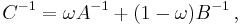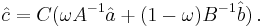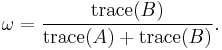Covariance intersection
Covariance intersection is an algorithm for combining two or more estimates of state variables in a Kalman filter when the correlation between them is unknown.[1][2][3]
Specification
Items of information a and b are known and are to be fused into information item c. We know a and b have mean/covariance 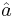 ,
,  and
and 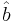 ,
,  , but the cross correlation is not known. The covariance intersection update gives mean and covariance for c as
, but the cross correlation is not known. The covariance intersection update gives mean and covariance for c as
The weighting coefficient ω is chosen so to have reasonable properties as the sizes of A and B vary: such a consideration gives[4]
Corresponding formulae for the combination of more than two estimates are available.[4]
References
- ^ Sonia Marques (2007)"Covariance intersection algorithm for formation flying spacecraft navigation from RF measurements", 4 ISLAB workshop, 12 November 2007
- ^ Simon J. Julier and Jeffrey K. Uhlmann (2007) "Using covariance intersection for SLAM" , Robotics and Autonomous Systems, 55,(7), 3-20
- ^ Lingji Chen, Pablo O. Arambel and Raman K. Mehra (2002) "Fusion under unknown correlation - Covariance intersection as a special case", International Society of Information Fusion Conference 2002
- ^ a b Niehsen, W., Bosch, R. (2002) Information Fusion based on Fast Covariance Intersection Filtering, International Society of Information Fusion Conference 2002